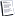Before somebody tells me there's something wrong with programs
LINE_ZIN and INPUT_Z I'd better put in a few words of explanation.

First of all there's nothing wrong with the programs. Both are
correct.

They both calculate the reflection coefficient Gamma for a given line
and given load impedance at a given frequency. One does it for coaxial
lines and the other for balanced-twin and open-wire lines.

But, believe it or not, under certain load conditions the reflection
coefficient Gamma can exceed unity. Indeed, at a sufficiently low
frequency, Gamma can approach 1+Sqrt(2) = 2.414

With program LINE_ZIN enter the following -

Freq = 0.2 MHz
Conductor diameter = 0.2 mm
Conductor spacing = 10 mm
Line length = 119.25 metres
Velocity factor = 1.00
Load resistance = 0.00 ohms
Load reactance = + 552.6 ohms

From which we get -

Zo = 552.6 ohms
Gamma = 1.084
Angle of Gamma = -90.0 degrees
SWR at load end = 24.8
SWR at input end = Infinity

With program INPUT_Z enter the following -

Frequ = 0.2 MHz
Zo = 50 ohms
Line length = 100 metres
Inner conductor diameter = 0.73 mm (RG-58)
Velocity factor = 0.66
Load resistance = 0.00 ohms
Load reactance = +50.00 ohms

From which we get -

Gamma = 1.109
Angle of Gamma = -90.0 degrees
SWR at load end = 19.3

The reason for the abnormally high values of Gamma, and the SWR at the
input end being higher than the SWR at the load end, is that the line
impedance Zo is not purely resistive. It has a negative angle. Zo =
Ro - jXo.

There is a resonance between -jXo and + jXload which causes the
reflected wave to be greater than the incident wave. Hence Gamma
exceeds unity. The effect is not present when jXload is negative.

Gamma has a maximum value when +Xload = Zo as can be found by varying
Xload on either side of Zo.

At some distance back from the load the extraordinary high value of
SWR occurs (as demonstrated with program LINE_ZIN) due to that point
taking the place of the end of the line when Zo is purely resistive.

The true value of Zo = Ro+jXo can be found by making the line long
enough such that attenuation exceeds about 35 or 40 dB. Line input
impedance is then becomes equal to Zo.

It is the fact that Zo is never purely resistive which causes errors
when using the Smith Chart. Errors which the user can be entirely
unaware of. Coax lines are more prone to error than higher impedance
balanced-twin lines.

The reason why both programs stop at 200 KHz has nothing to do with
the foregoing. It is due to skin effect not being fully operative at
lower frequencies which complicates calculations.
There are other programs which go down to audio and power frequencies.
----
Reg, G4FGQ